To talk about parallel lines we first must understand the definition of line. A line is a succession of infinite points in the same direction. This succession is characterized by being continuous and indefinite. For this reason, we say that a line has neither a beginning nor an end.
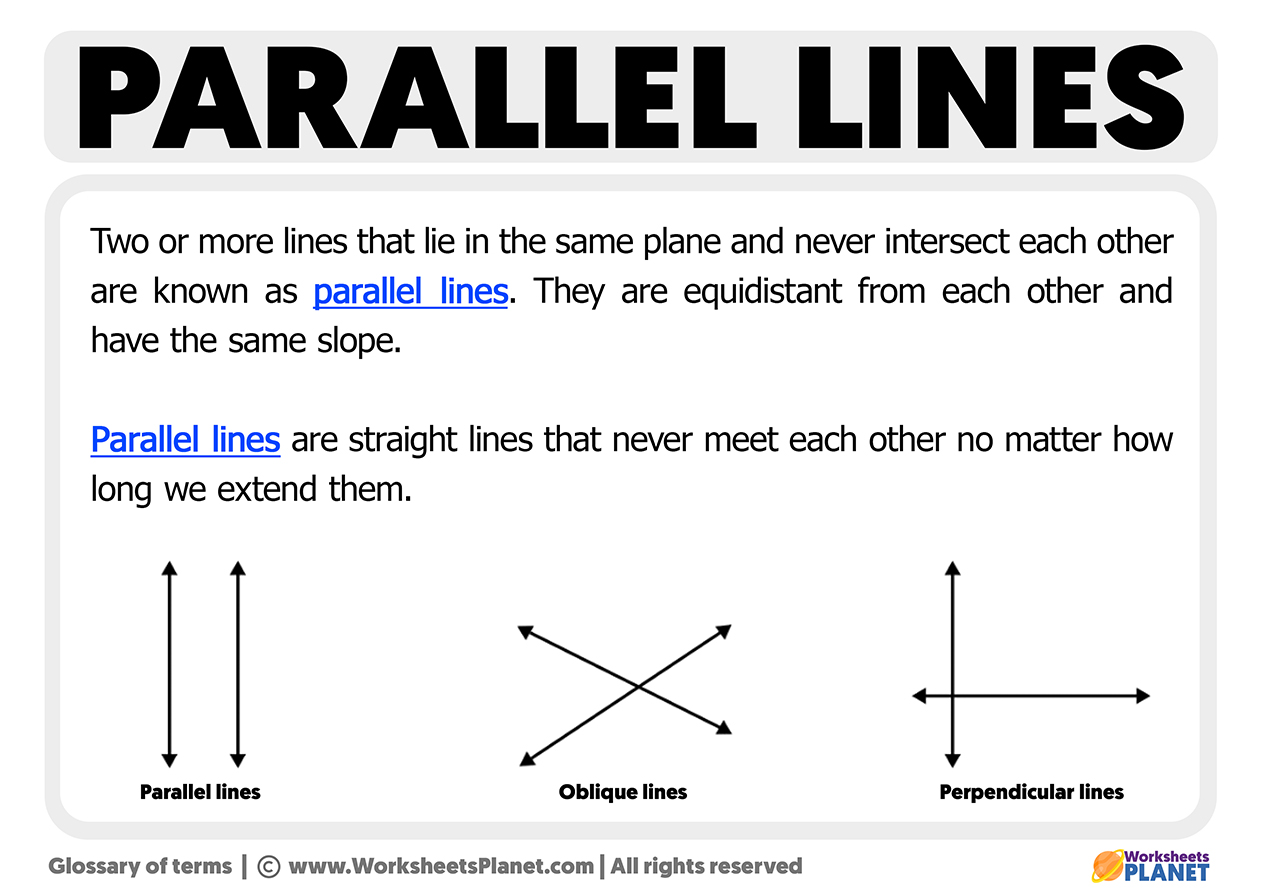
Parallel lines are two lines that are in the same plane but they never intersect. Two lines in a plane are parallel if they are the same line or, on the contrary, if they do not share any point in common. Similarly, they can be similar in space if they are on the same plane or do not share any points.
Parallel lines are lines that maintain a certain distance from each other, and even though they can extend their trajectory to infinity, they can never meet or touch at any point. Parallel lines cannot touch or cross; not even their extensions can cross each other. Train tracks are a clear example of parallel lines we can in our daily routine life.
Characteristics of Parallel Lines
- They are always at the same distance but never touch each other.
- Parallel lines or straight lines are always pointing in the same direction.
- When the parallel lines intersect with another line, which is known as the Transversal, it can be seen that the angles are equal.
- Parallel lines have a pair of corresponding and equal angles.
- They have a pair of alternate interior angles of equal measure.

